Introduction
Overdrive is at the heart of modern guitar playing. We all know what it sounds like; from the hint of breakup as tubes begin saturating, to the mighty crunch and roar of an amp being pushed by a boost pedal. Whether you play blues, rock, psych, metal or industrial-post-noise-core, you’ll need an overdrive which can give you what you’re looking for.
Understanding the causes and characteristics of overdrive in amplifier electronics is crucial to making a quality pedal that delivers versatile overdrive. In this article, we show you some of our research and inspiration for development of our algorithms.
The first section will show analysis of a classic solid state overdrive circuit and how the Vector Drive distortion pedal models this effect. The second half of the post will look at measurements from a tube amplifier pushed into saturation along with the Vector Drive’s wave shaping feature which can mimic this.
Classic Overdrive Pedal Analysis
Lets begin this section by looking at the core of traditional overdrive pedal circuits. Below is a typical overdrive clipping circuit, such as that in the Tube Screamer, built in LTSpice. The circuit has been simplified by removing all frequency dependent components and using ideal diodes and op-amp. As with our fuzz analysis we’re stripping everything back to its core to understand the essence of an effect, not copy an existing product.
NB: Non-ideal (ie: real) diodes produce a much smoother clipping than is presented here but ideal diodes make the circuit’s underlying behaviour easier to see.
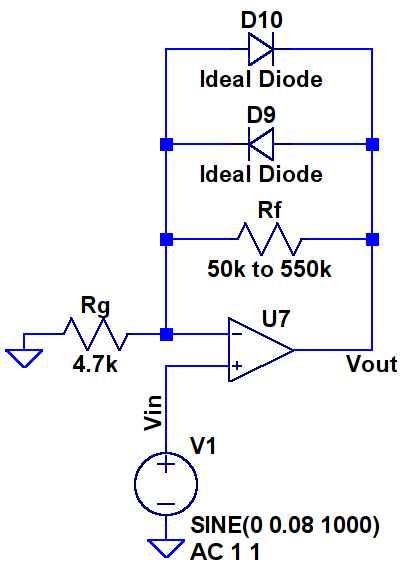 The circuit above is based around an op-amp in a so-called non-inverting topology which, without the diodes, has a gain of:
The circuit above is based around an op-amp in a so-called non-inverting topology which, without the diodes, has a gain of:
(1) 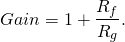
The resistor 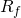 is what is adjusted when turning the gain knob on an overdrive pedal.
is what is adjusted when turning the gain knob on an overdrive pedal.
If the diodes are ignored and the typical 50k to 550k resistance range is used the circuit above has a gain of between 9.5 and 118, or approximately 20dB to 41dB. With this much gain a typical 300mV guitar signal would be amplified to between 3V and 30V, enough for the op-amp’s output to hard clip near its power supply voltage (typically 0-9V). We will see later that situation is avoided by the diodes.
For the following analysis we will assume the diodes are ideal, this means that if their forward voltage is below some threshold, we chose 0.6V, their resistance is infinite and if it is above 0.6V their resistance becomes zero.
The diodes avoid hard clipping by reducing the circuit’s gain when the output reaches a certain amplitude. The gain reduction occurs because when one of them conducts the effective value of 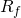 drops to zero, causing unity gain as per the equation above.
drops to zero, causing unity gain as per the equation above.
Given that the diodes conduct when their voltage exceeds 0.6V we need a way of finding their terminal voltage as a function of 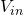 . The voltage across the diodes can by calculated by noting the characteristics of ideal op-amps and concluding that the inverting (-) and non-inverting (+) inputs of the op-amp will always be the same voltage. Therefore we claim that the op-amp’s inputs will both be equal to
. The voltage across the diodes can by calculated by noting the characteristics of ideal op-amps and concluding that the inverting (-) and non-inverting (+) inputs of the op-amp will always be the same voltage. Therefore we claim that the op-amp’s inputs will both be equal to 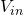 (the input voltage) and, considering the case where
(the input voltage) and, considering the case where 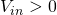 the diode D9 will conduct when:
the diode D9 will conduct when:
(2) 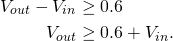
The same logic can be used to derive the equation for D10’s conduction threshold as 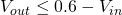 but the proof is left as an exercise for the reader.
but the proof is left as an exercise for the reader.
Given equation 2 and the fact that a conducting diode drops 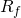 to zero (and the gain to 1) we can conclude that if D9 is conducting then
to zero (and the gain to 1) we can conclude that if D9 is conducting then 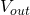 is, in fact, equal to
is, in fact, equal to 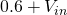 . ie: the output is clamped by the diode’s conduction threshold.
. ie: the output is clamped by the diode’s conduction threshold.
The diode’s conduction requirement can be written in terms of 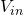 by observing that:
by observing that:
(3) 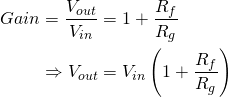
and substituting this expression for 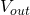 into equation 2:
into equation 2:
(4) 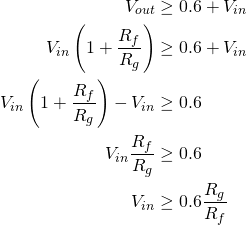
We can now write a complete set of equations for the overdrive circuit:
(5) 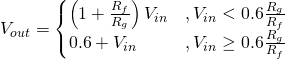
So, if the input is driven with a sine wave the general shape of the output is shown below:
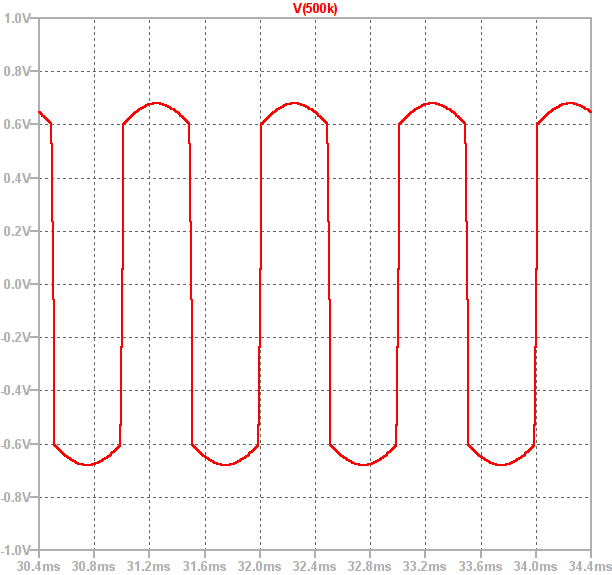
It can be seen that between approximately -0.6V and 0.6V the output is a sine wave which has been amplified with high gain. However, as soon as the output exceeds 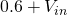 the diodes conduct and the gain drops to 1. This causes the output to follow the input, shifted by +/- 0.6V. This creates smooth peaks instead of a hard clipped square wave.
the diodes conduct and the gain drops to 1. This causes the output to follow the input, shifted by +/- 0.6V. This creates smooth peaks instead of a hard clipped square wave.
Another way of visualising the circuit’s behaviour is by plotting the input signal’s amplitude on the x-axis and the corresponding output amplitude on the y-axis to create a graph of the circuit’s static non-linearity. The plot below shows this for three different values of 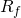 :
:
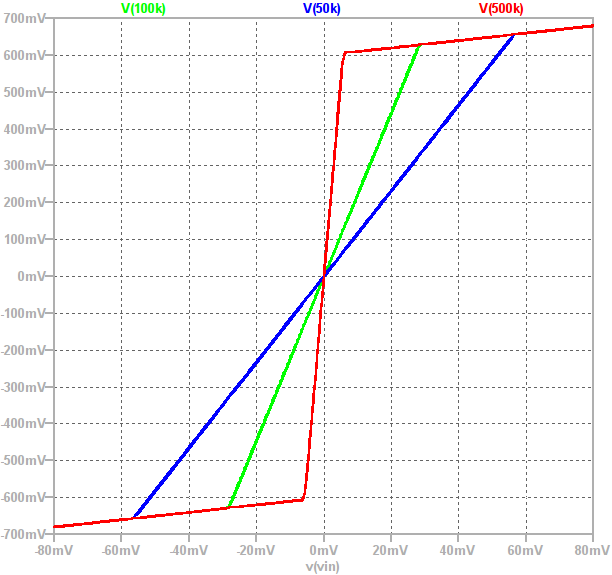
Observe that the “knee point” is at 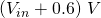 . The gain of a circuit is equal to the gradient of the above plot and the two gain “regions” can clearly be seen. The gain is high when the output is between
. The gain of a circuit is equal to the gradient of the above plot and the two gain “regions” can clearly be seen. The gain is high when the output is between 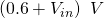 and
and 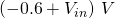 then suddenly drops to 1 once one of the diodes conducts.
then suddenly drops to 1 once one of the diodes conducts.
The broad effect of this circuit is a type of smooth clipping where the “smoothness” comes from the clean input being mixed in with the distorted output. This is, in fact, the core feature of overdrive: it is a saturated signal with some clean input mixed back in.
This can be seen from the circuit’s gain equation:
(6) 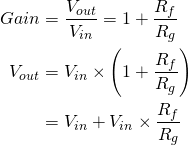
One way of looking at the circuit’s two operating regions is to imagine the value of 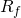 varying with the input voltage. This equation then informally shows that the output,
varying with the input voltage. This equation then informally shows that the output, 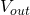 is equal to the clean input,
is equal to the clean input, 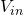 plus a high gain copy of it where the high gain signal gets saturated (clipped) at the diode’s forward voltage. This supports the statement above that the overdrive effect is a saturated version of the input with some of the clean input mixed over the top.
plus a high gain copy of it where the high gain signal gets saturated (clipped) at the diode’s forward voltage. This supports the statement above that the overdrive effect is a saturated version of the input with some of the clean input mixed over the top.
The Vector Drive’s Overdrive Implementation
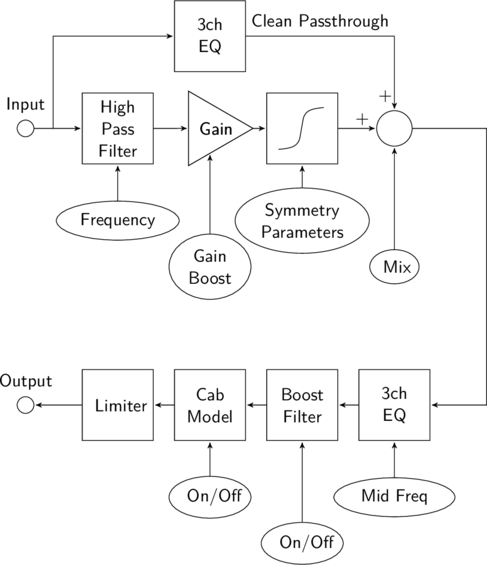
The basic signal chain of the Vector Drive’s overdrive effect is shown below:
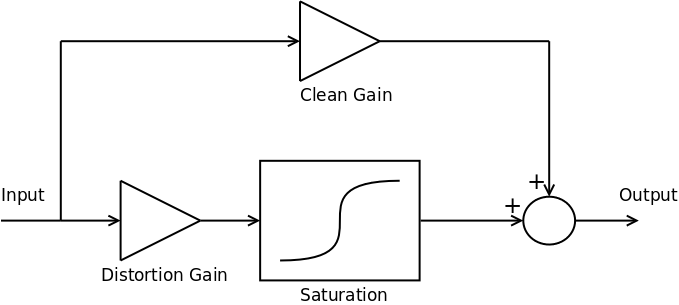
The full signal chain contains several filter blocks (such as the main 3 channel parametric tone controls) but these have been omitted for clarity.
In traditional overdrive pedals the distortion gain level, set by 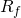 , is adjustable. In the Vector Drive, however, the versatility of DSP allows for both the distortion gain and clean gain to be set by the player.
, is adjustable. In the Vector Drive, however, the versatility of DSP allows for both the distortion gain and clean gain to be set by the player.
In our DSP code the saturation function is the smooth clipping equation:
(7) 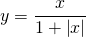
which, when mixed with the clean signal, results in waveforms such as the one below; a beautifully smooth clipped sine wave:
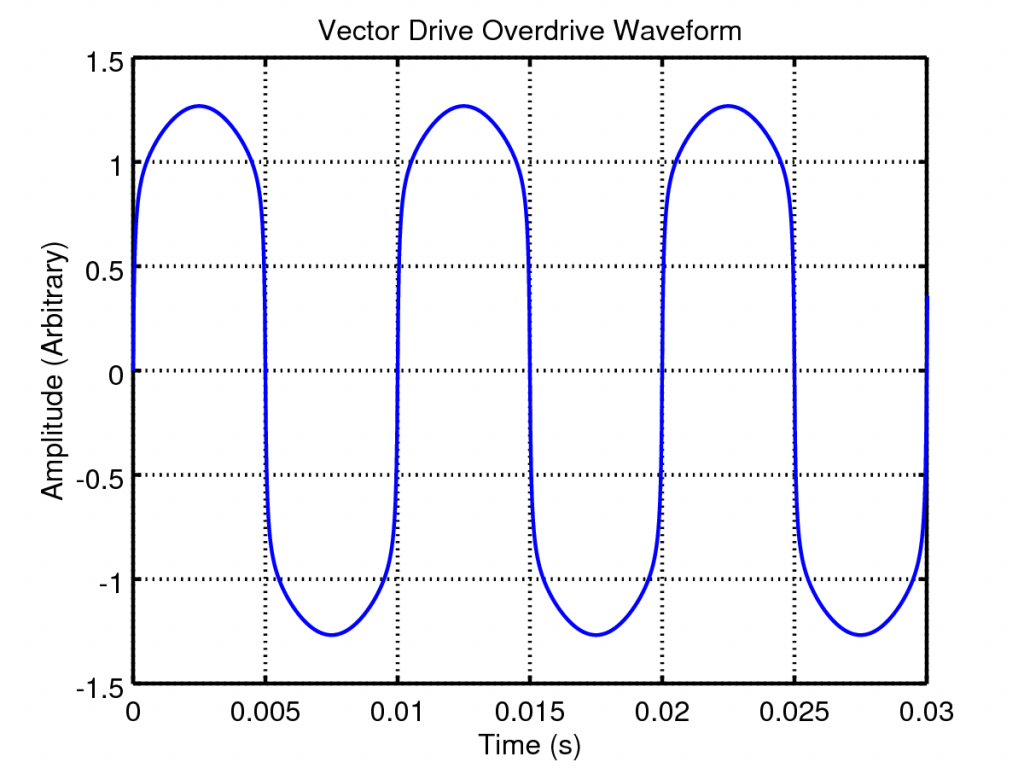 So lets look at the effect of varying the distortion and clean gains. If we plot the above waveform shaping as a static non-linearity and vary the distortion gain we get the following plots:
So lets look at the effect of varying the distortion and clean gains. If we plot the above waveform shaping as a static non-linearity and vary the distortion gain we get the following plots:
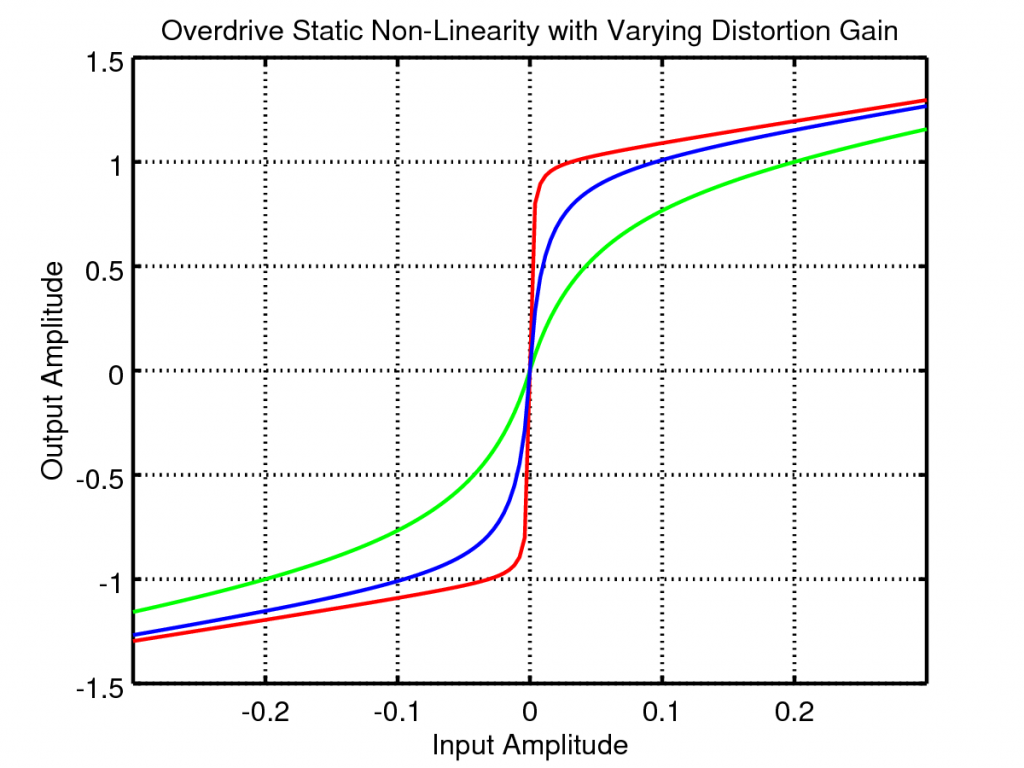 The distortion gain adjusts the underlying tonal mix of the output, increasing this gain creates higher frequency harmonics leading to a more crunchy sound.
The distortion gain adjusts the underlying tonal mix of the output, increasing this gain creates higher frequency harmonics leading to a more crunchy sound.
If, instead, we vary the clean mix the static non-linearity changes as follows:
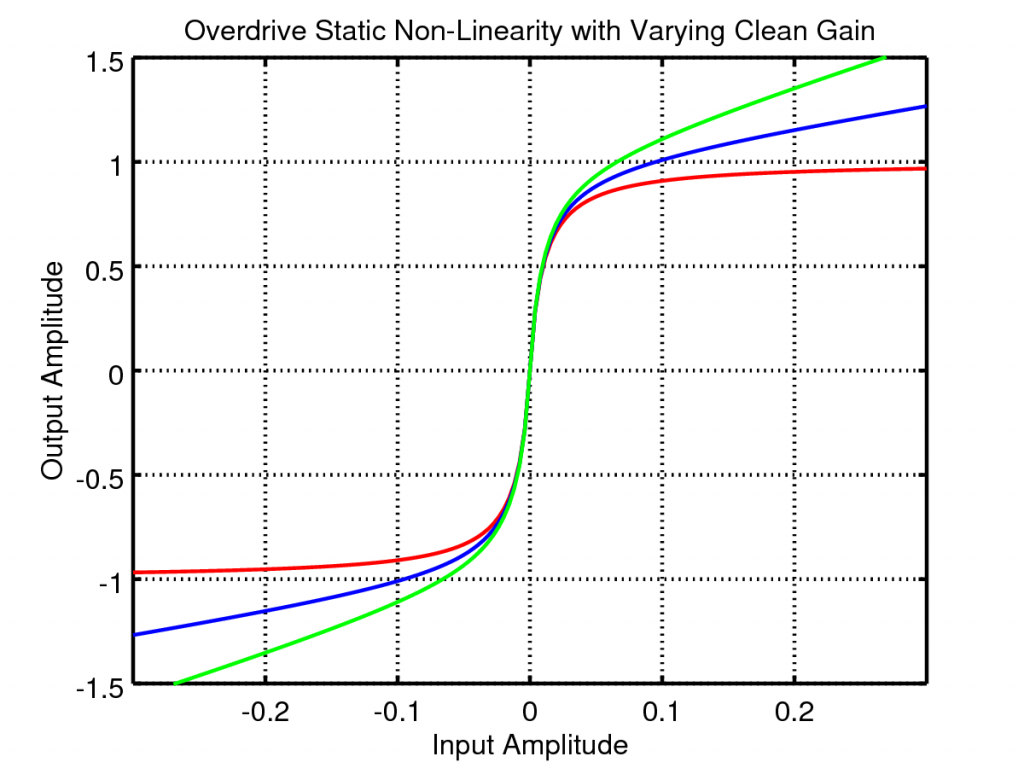
With this adjustment the output can be varied from totally saturated hard core distortion to super subtle overdrive.

 The circuit above is based around an op-amp in a so-called
The circuit above is based around an op-amp in a so-called 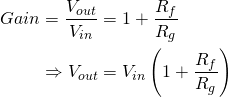
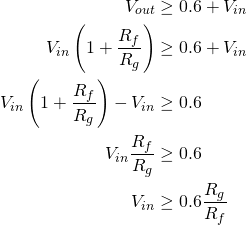
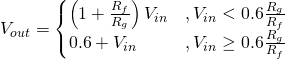


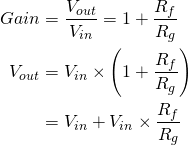

 So lets look at the effect of varying the distortion and clean gains. If we plot the above waveform shaping as a static non-linearity and vary the distortion gain we get the following plots:
So lets look at the effect of varying the distortion and clean gains. If we plot the above waveform shaping as a static non-linearity and vary the distortion gain we get the following plots: The distortion gain adjusts the underlying tonal mix of the output, increasing this gain creates higher frequency harmonics leading to a more crunchy sound.
The distortion gain adjusts the underlying tonal mix of the output, increasing this gain creates higher frequency harmonics leading to a more crunchy sound.