The Vector Drive’s Audio Signal Chain

Recently we recorded a video which demonstrates many of the Vector Drive’s capabilities. It’s a great resource if you’re keen to see a mix of distortion, overdrive and fuzz tones created by the pedal.

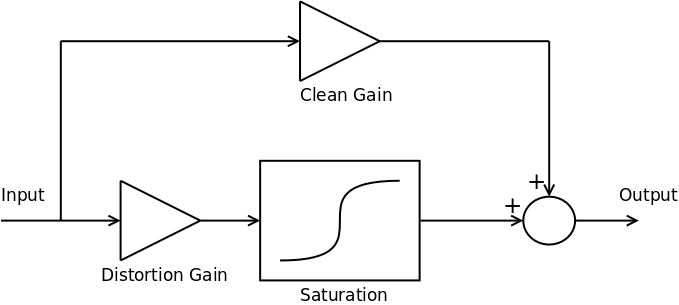
But how are all these tones made? To learn about the Vector Drive’s audio processing capabilities we’ve sketched up the following diagram:

Rendered by QuickLaTeX.com

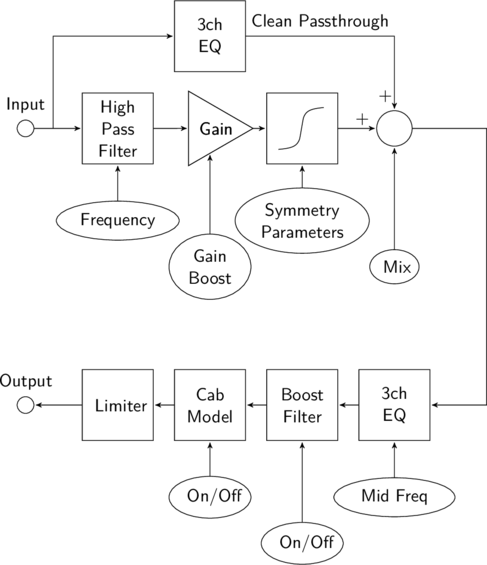
The squares (and gain triangle) represent processing blocks while the ellipses are settings you have control over. The output volume, bass/mid/treble EQ and gain controls are omitted for clarity but, as a guitarist, hopefully you have a feel for what those knobs do.

Distortion Block

In the diagram’s top half you can see the effects main purpose: gain and saturation (the ‘s’ shaped block). This is modelling amplifier clipping and is what creates distortion; everything else in the processing chain shapes the tone to your taste. The “gain boost” kicks in when you hit the boost switch and, along with a bit of tone tweaking, makes your playing jump out from the rest of the band.

Before the distortion we’ve placed a high pass filter, this removes bass from the audio before it gets distorted. Exactly how much bass is controlled by a frequency cut-off parameter. Notes below this frequency are removed and the rest allowed the pass.

A low cut-off frequency keeps the bass, allowing creation of a classic 70s fuzz tone, while increasing the cut-off frequency removes it and makes the output more “scratchy”. The cut-off can go all the way down to 20Hz so the Vector Drive is suitable for bass guitar too!

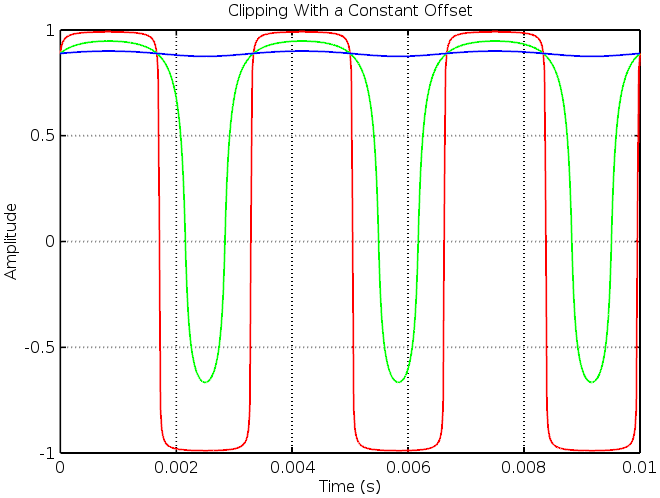
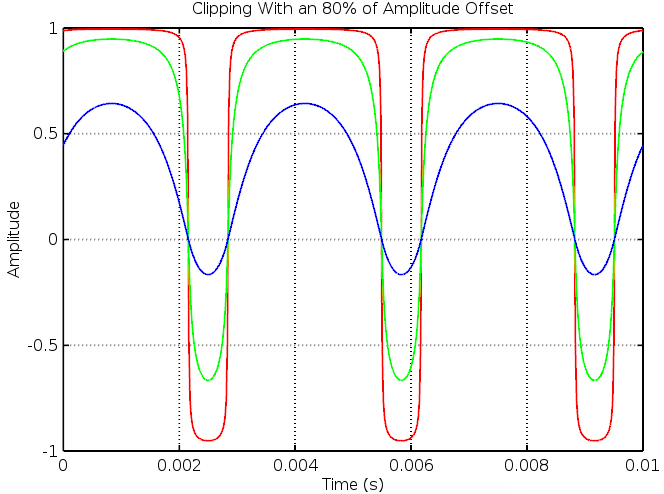
There are two symmetry parameters, one of which is discussed at length in the fuzz article and another which clips the top half of the wave more than the bottom, leading to an overdrive-like tone. We’ll be writing more about that one in a future article.

Clean Mix

Above the distortion section is a 3 channel EQ which is applied to the clean signal. This EQ’ed clean audio is then mixed in with the distorted signal to create overdrive effects. This is discussed at length in our overdrive article but in short it mimics the sound of classic overdrive pedals.

The clean/distorted mix is smoothly adjustable for maximum control. You can, for example, remove all the bass from the distortion with the high pass filter then mix in clean bass by adjustment of the clean EQ. This can avoid the distortion sounding “muddy”, which can happen if too much bass goes through the clipping section, but keeps bass in the output.

Post-Processing

Output Equalizer

In the diagram’s lower half we start with another 3 channel EQ but this time the mid frequency is adjustable. Setting the mid frequency to around 700Hz lets you create a brutal scooped mids tone or it can be turned up and boosted to really cut through the mix for a shredding solo.

Boost Filter

Next comes the boost filter. Activating boost not only gives you more gain but also increases the presence of your sound. This is a switchable increase of the upper-mids which makes your tone clearer and more “present”.

Speak Cabinet Emulation

After the boost filter comes the cab model which is detailed in an earlier article. This is a filter which emulates the tone of a real guitar speaker cabinet, allowing the Vector Drive to sound like a real amp when practicing with headphones, recording or even playing at a live gig.

Output Limiter

Finally there’s an output limiter. This stops the output from hard clipping when turned up too loud. When the limiter is engaged the indicator LED flashes rapidly. If the limiter is activated occasionally it isn’t a major issue but the output volume should be dropped if it is always on.

Final Words

If you haven’t seen the video yet you can check it out at the top of this post or here on our Facebook. The Vector Drive is scheduled for release in late 2017 or early 2018, we’ll keep you updated via the Facebook page.

September 12, 2017September 20, 2017

Overdrive: What is it and how is it implemented in the Vector Drive? Part One

Introduction

Overdrive is at the heart of modern guitar playing. We all know what it sounds like; from the hint of breakup as tubes begin saturating, to the mighty crunch and roar of an amp being pushed by a boost pedal. Whether you play blues, rock, psych, metal or industrial-post-noise-core, you’ll need an overdrive which can give you what you’re looking for.

Understanding the causes and characteristics of overdrive in amplifier electronics is crucial to making a quality pedal that delivers versatile overdrive. In this article, we show you some of our research and inspiration for development of our algorithms.

The first section will show analysis of a classic solid state overdrive circuit and how the Vector Drive distortion pedal models this effect. The second half of the post will look at measurements from a tube amplifier pushed into saturation along with the Vector Drive’s wave shaping feature which can mimic this.

Classic Overdrive Pedal Analysis

Lets begin this section by looking at the core of traditional overdrive pedal circuits. Below is a typical overdrive clipping circuit, such as that in the Tube Screamer, built in LTSpice. The circuit has been simplified by removing all frequency dependent components and using ideal diodes and op-amp. As with our fuzz analysis we’re stripping everything back to its core to understand the essence of an effect, not copy an existing product.

NB: Non-ideal (ie: real) diodes produce a much smoother clipping than is presented here but ideal diodes make the circuit’s underlying behaviour easier to see.

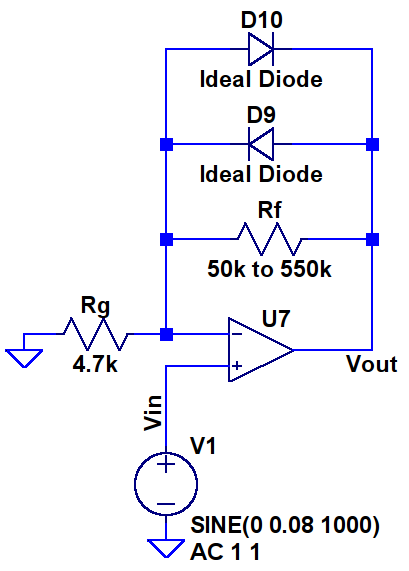The circuit above is based around an op-amp in a so-called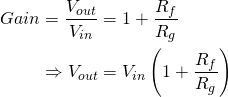 non-inverting topology which, without the diodes, has a gain of:

(1) $\begin{equation*}Gain=1 + \frac{R_f}{R_g}.\end{equation*}$

The resistor $R_f$ is what is adjusted when turning the gain knob on an overdrive pedal.

If the diodes are ignored and the typical 50k to 550k resistance range is used the circuit above has a gain of between 9.5 and 118, or approximately 20dB to 41dB. With this much gain a typical 300mV guitar signal would be amplified to between 3V and 30V, enough for the op-amp’s output to hard clip near its power supply voltage (typically 0-9V). We will see later that situation is avoided by the diodes.

For the following analysis we will assume the diodes are ideal, this means that if their forward voltage is below some threshold, we chose 0.6V, their resistance is infinite and if it is above 0.6V their resistance becomes zero.

The diodes avoid hard clipping by reducing the circuit’s gain when the output reaches a certain amplitude. The gain reduction occurs because when one of them conducts the effective value of $R_f$ drops to zero, causing unity gain as per the equation above.

Given that the diodes conduct when their voltage exceeds 0.6V we need a way of finding their terminal voltage as a function of $V_{in}$ . The voltage across the diodes can by calculated by noting the characteristics of ideal op-amps and concluding that the inverting (-) and non-inverting (+) inputs of the op-amp will always be the same voltage. Therefore we claim that the op-amp’s inputs will both be equal to $V_{in}$ (the input voltage) and, considering the case where $V_{in} > 0$ the diode D9 will conduct when:

(2) $\begin{align*} V_{out} -V_{in} &\geq 0.6 \\ V_{out} &\geq 0.6 + V_{in}.\end{align*}$

The same logic can be used to derive the equation for D10’s conduction threshold as $V_{out} \leq 0.6 - V_{in}$ but the proof is left as an exercise for the reader.

Given equation 2 and the fact that a conducting diode drops $R_f$ to zero (and the gain to 1) we can conclude that if D9 is conducting then $V_{out}$ is, in fact, equal to $0.6 + V_{in}$ . ie: the output is clamped by the diode’s conduction threshold.

The diode’s conduction requirement can be written in terms of $V_{in}$ by observing that:

(3) $\begin{align*}Gain &= \frac{V_{out}}{V_{in}} = 1 + \frac{R_f}{R_g} \\ &\Rightarrow V_{out} = V_{in}\left(1 + \frac{R_f}{R_g}\right)\end{align*}$

and substituting this expression for $V_{out}$ into equation 2:

(4) $\begin{align*} V_{out} &\geq 0.6 + V_{in} \\ V_{in}\left(1 + \frac{R_f}{R_g}\right) &\geq 0.6 + V_{in} \\ V_{in}\left(1 + \frac{R_f}{R_g}\right) - V_{in} &\geq 0.6 \\ V_{in} \frac{R_f}{R_g} &\geq 0.6 \\ V_{in} &\geq 0.6 \frac{R_g}{R_f} \end{align*}$

We can now write a complete set of equations for the overdrive circuit:

(5) $\begin{equation*} V_{out} = \begin{cases} \left( 1 + \frac{R_f}{R_g} \right)V_{in} &, V_{in} < 0.6 \frac{R_g}{R_f} \\ 0.6 + V_{in} &,V_{in} \geq 0.6 \frac{R_g}{R_f} \end{cases} \end{equation*}$

So, if the input is driven with a sine wave the general shape of the output is shown below:

It can be seen that between approximately -0.6V and 0.6V the output is a sine wave which has been amplified with high gain. However, as soon as the output exceeds $0.6+V_{in}$ the diodes conduct and the gain drops to 1. This causes the output to follow the input, shifted by +/- 0.6V. This creates smooth peaks instead of a hard clipped square wave.

Another way of visualising the circuit’s behaviour is by plotting the input signal’s amplitude on the x-axis and the corresponding output amplitude on the y-axis to create a graph of the circuit’s static non-linearity. The plot below shows this for three different values of $R_f$ :

Observe that the “knee point” is at $(V_{in}+0.6)~V$ . The gain of a circuit is equal to the gradient of the above plot and the two gain “regions” can clearly be seen. The gain is high when the output is between $\left(0.6 + V_{in}\right)~V$ and $(-0.6 + V_{in})~V$ then suddenly drops to 1 once one of the diodes conducts.

The broad effect of this circuit is a type of smooth clipping where the “smoothness” comes from the clean input being mixed in with the distorted output. This is, in fact, the core feature of overdrive: it is a saturated signal with some clean input mixed back in.

This can be seen from the circuit’s gain equation:

(6) $\begin{align*}Gain &= \frac{V_{out}}{V_{in}} = 1 + \frac{R_f}{R_g} \\ V_{out} &= V_{in} \times \left(1 + \frac{R_f}{R_g}\right) \\ &= V_{in} + V_{in} \times \frac{R_f}{R_g}\end{align*}$

One way of looking at the circuit’s two operating regions is to imagine the value of $R_f$ varying with the input voltage. This equation then informally shows that the output, $V_{out}$ is equal to the clean input, $V_{in}$ plus a high gain copy of it where the high gain signal gets saturated (clipped) at the diode’s forward voltage. This supports the statement above that the overdrive effect is a saturated version of the input with some of the clean input mixed over the top.

The Vector Drive’s Overdrive Implementation

The basic signal chain of the Vector Drive’s overdrive effect is shown below:

The full signal chain contains several filter blocks (such as the main 3 channel parametric tone controls) but these have been omitted for clarity.

In traditional overdrive pedals the distortion gain level, set by $R_f$ , is adjustable. In the Vector Drive, however, the versatility of DSP allows for both the distortion gain and clean gain to be set by the player.

In our DSP code the saturation function is the smooth clipping equation:

(7) $\begin{equation*}y = \cfrac{x}{1 + \left| x \right|}\end{equation*}$

which, when mixed with the clean signal, results in waveforms such as the one below; a beautifully smooth clipped sine wave:

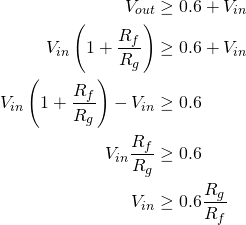
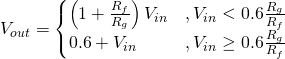
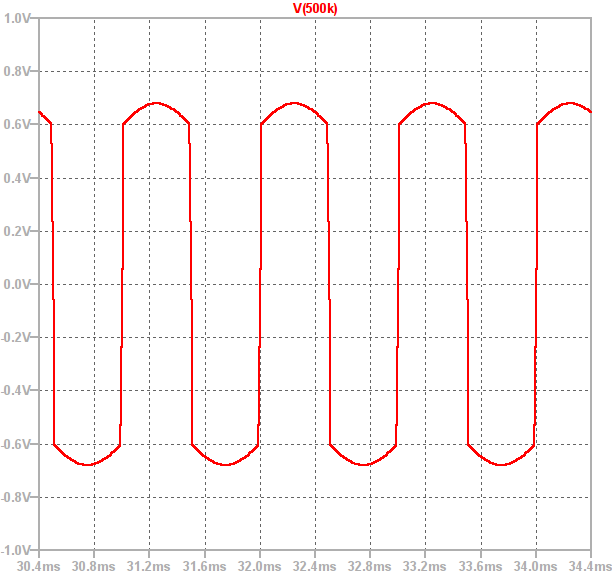
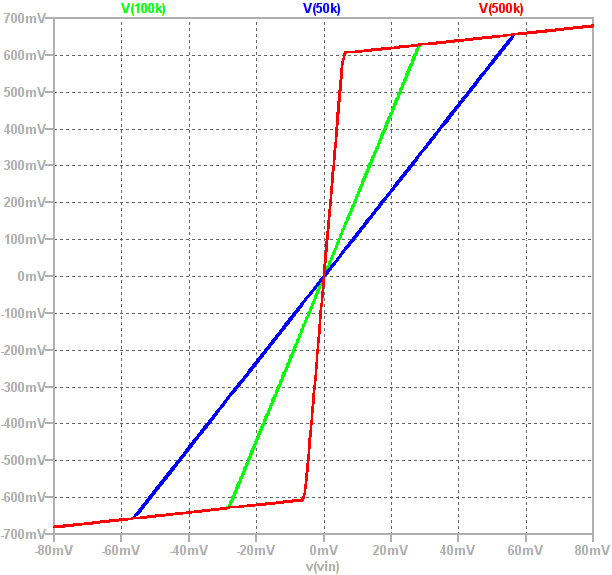
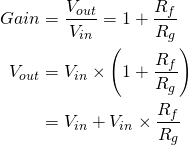
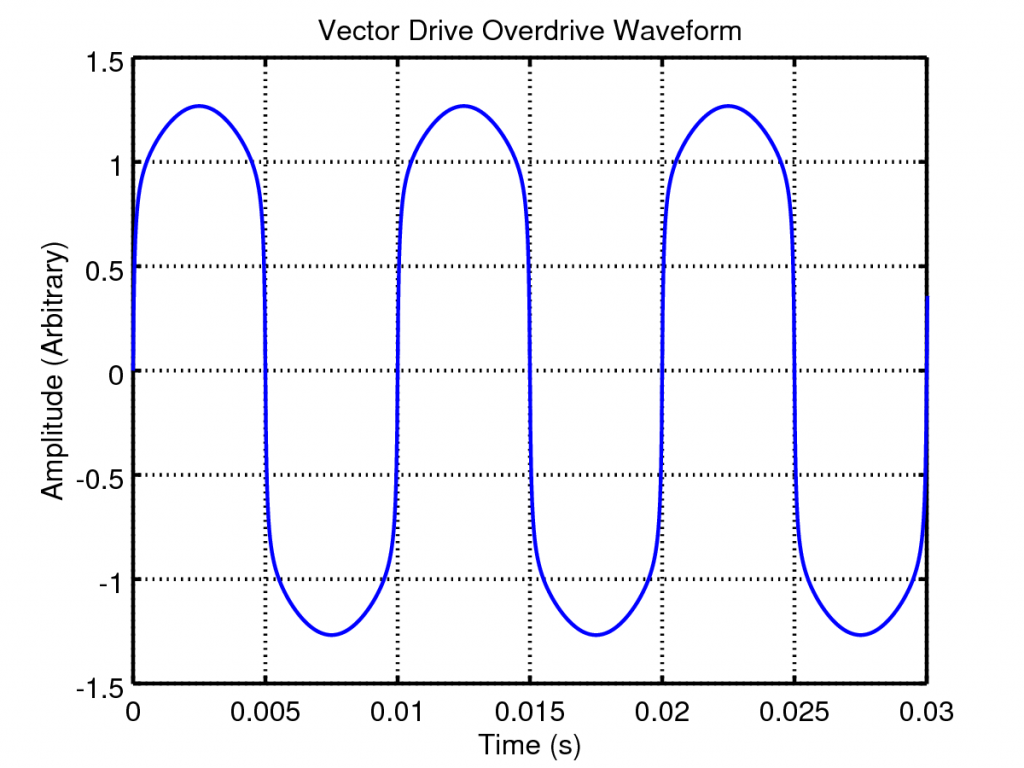So lets look at the effect of varying the distortion and clean gains. If we plot the above waveform shaping as a static non-linearity and vary the distortion gain we get the following plots:

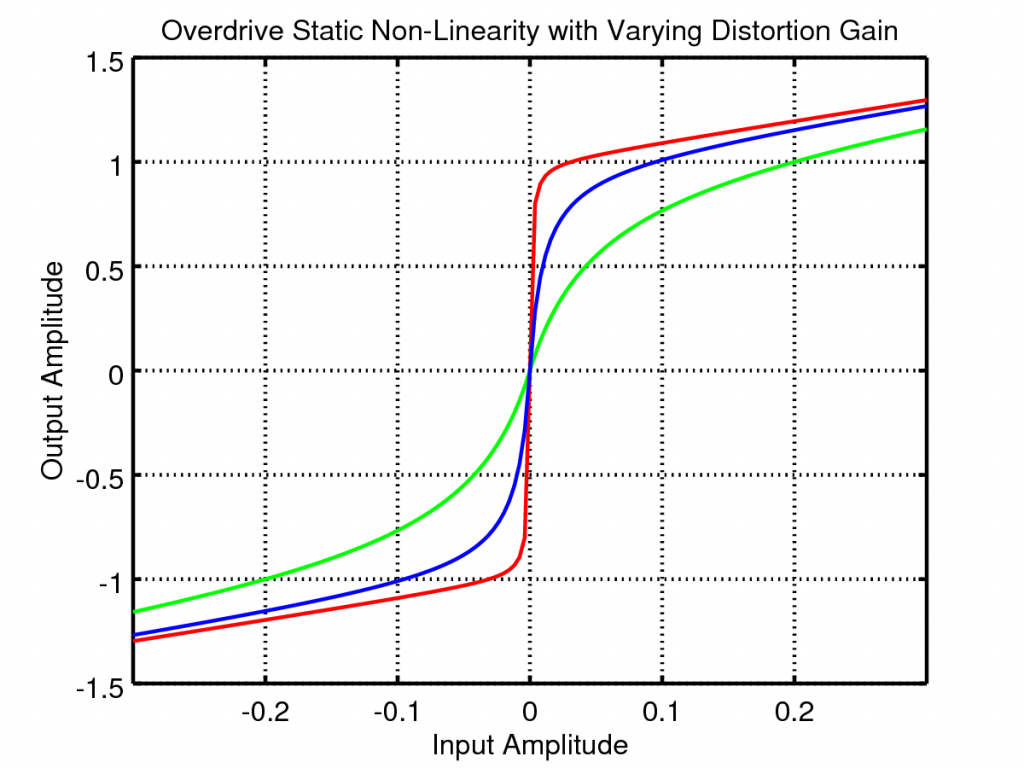The distortion gain adjusts the underlying tonal mix of the output, increasing this gain creates higher frequency harmonics leading to a more crunchy sound.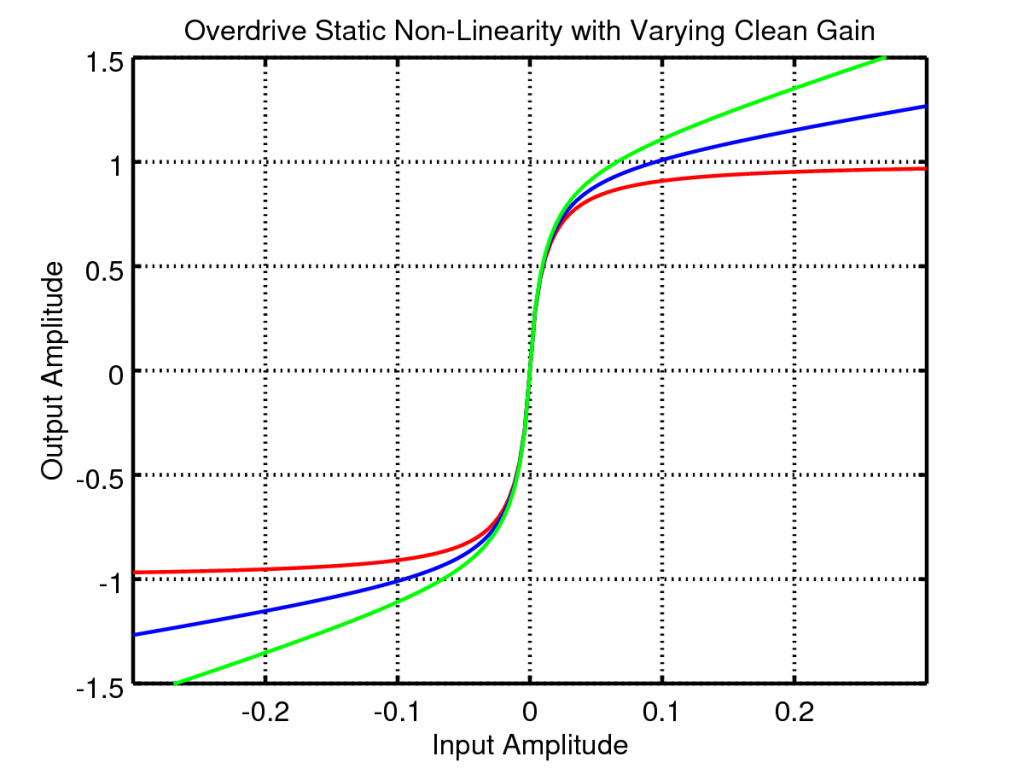

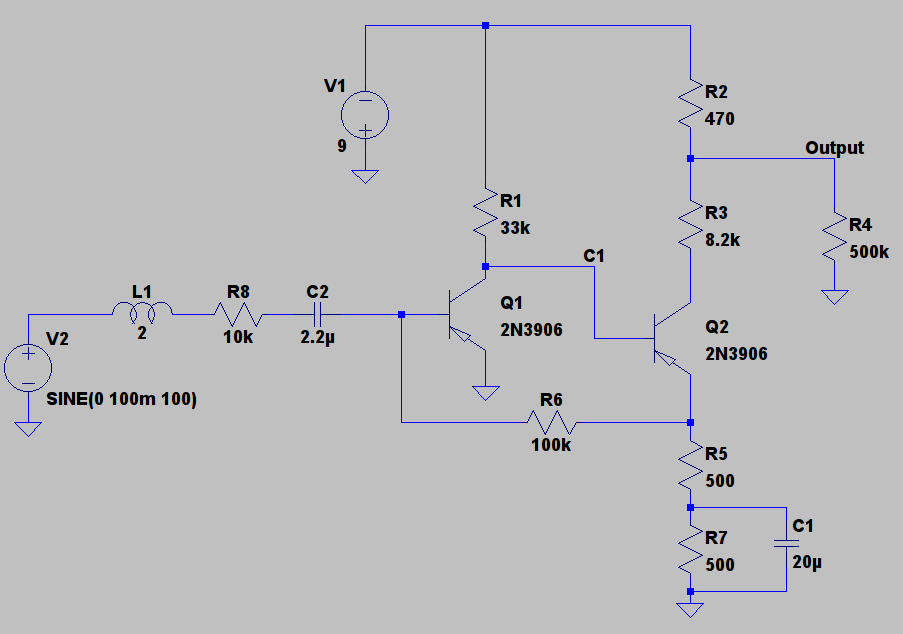
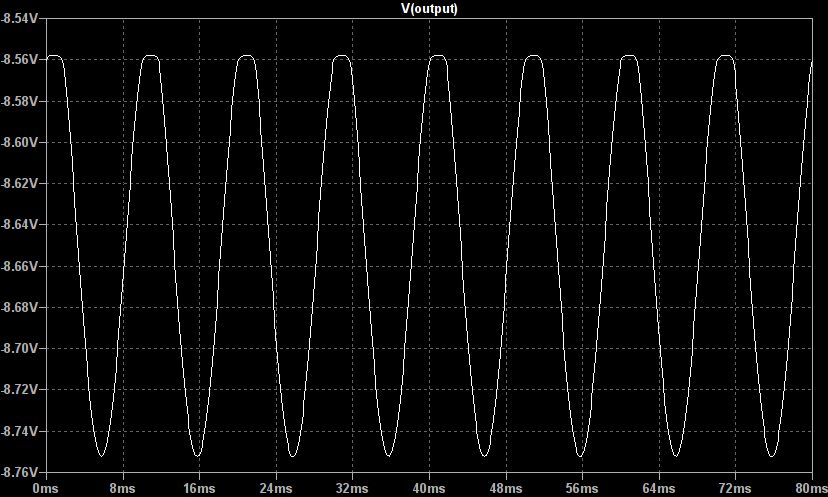
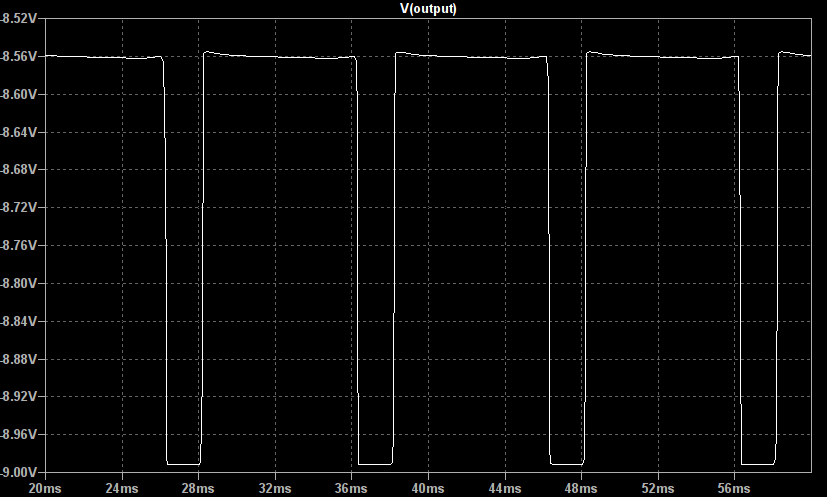
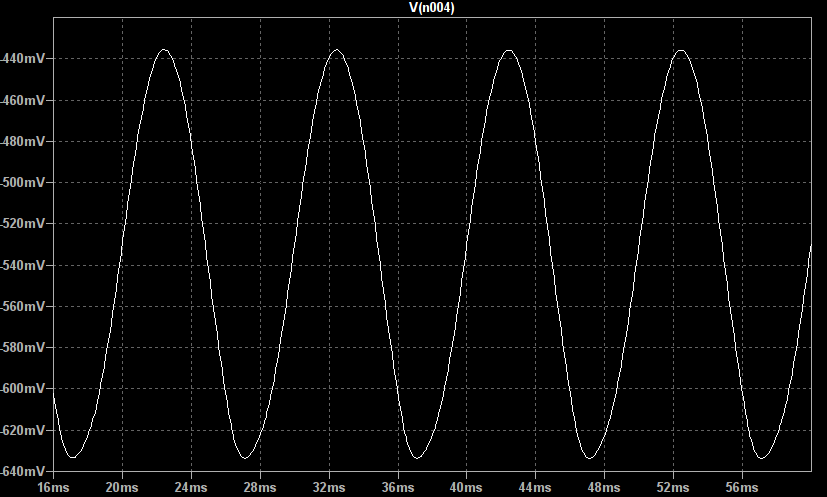
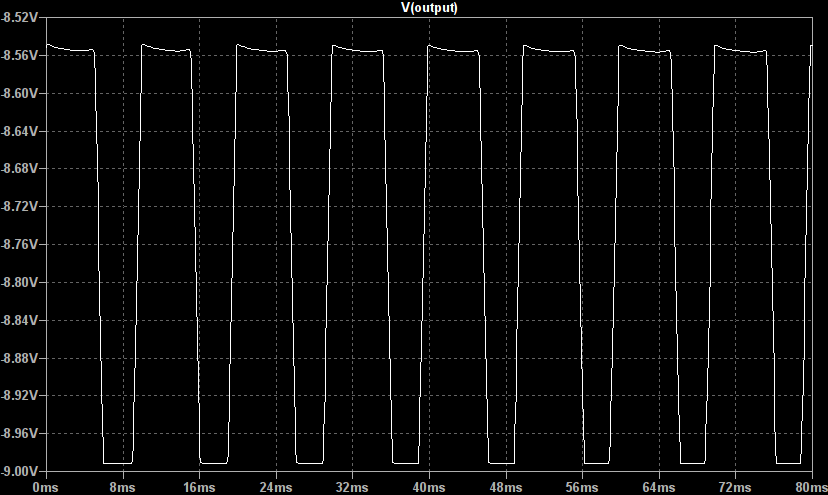
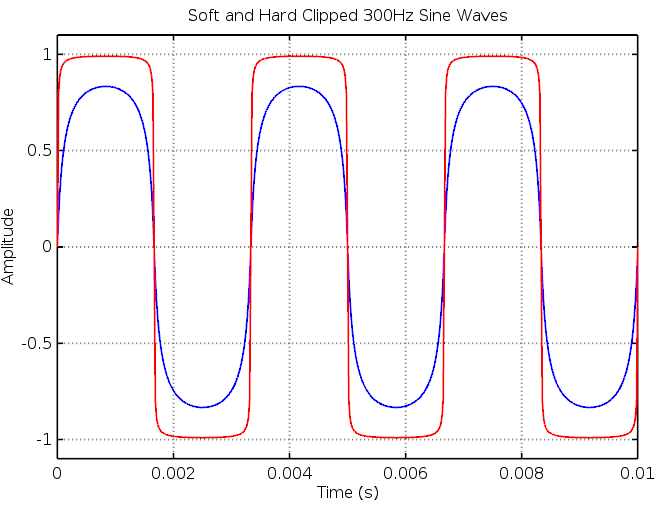
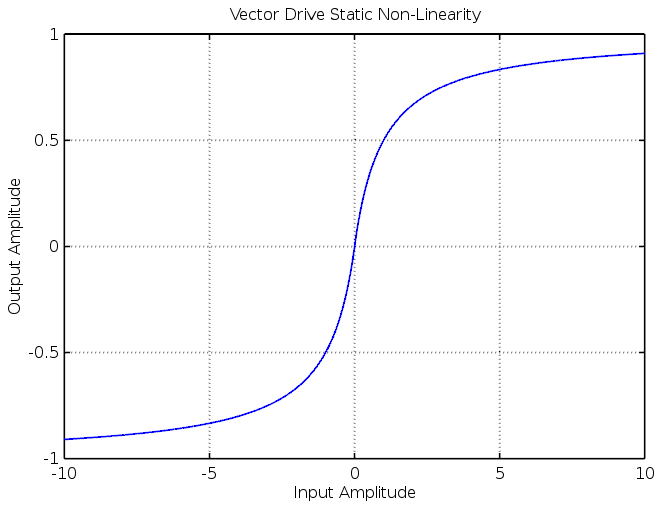If, instead, we vary the clean mix the static non-linearity changes as follows:

With this adjustment the output can be varied from totally saturated hard core distortion to super subtle overdrive.

September 4, 2017September 20, 2017

Modelling Fuzz

Introduction

Classic fuzz circuits, such as the one found in the original Fuzz Face pedal, created a unique style of asymmetric clipping which gave them their signature fuzzy feel. In this post we’ll be looking at the circuit feature which caused their hard clipped output waveforms to be asymmetric and how the Vector Drive can be used to recreate classic fuzz tones. We also demonstrate some sample audio and show how these features really sound.

We’d like to give a shout out to the excellent analysis of the Fuzz Face done by Electro Smash. Their articles were invaluable while designing the Vector Drive.

Fuzz Face Analysis

For this section we built the Fuzz Face circuit in LTSpice, a free (no cost, closed source) circuit simulation package from Linear Technology. The original Fuzz Face used the AC128 germanium PNP transistor, a device which doesn’t have a manufacture-published SPICE model (unless you trust random forum posts). As such we substituted The AC128 with a modern 2N3906 silicon PNP transistor. The results won’t exactly match the real circuit (the AC128s were highly variable anyway) but we aren’t trying to copy the Fuzz Face, just observe its general clipping style.

You can find our LTSpice circuit here. Note that it includes a 2H inductor and 10k Ohm resistor modelling the source impedance of a guitar pickup. These are typical values, if you can find data on your own pickup they can be adjusted to your needs. Note that active pickups, such as the classic EMG81, will have a purely resistive output impedance requiring the removal of L1.

The characteristic we’re interested in here is the shape of the output waveform at low and high input levels. Driven with a 1mV sine wave the output below shows a little clipping and is amplified to around 200mV p-p:

However, when driven with a larger 100mV signal the output shows obvious hard clipping and is strongly asymmetric, spending much of its time clipped high with only short bursts clipped low:

NB: The above plot was made with the pickup source impedance removed.

The source of this asymmetry is the way the input signal is coupled into the base of Q1, the first transistor. When driven with a 100mV sine wave the voltage at this point is only below the ~600mV base conduction threshold for a small amount of time at the bottom of each cycle:

It is crucial to note that here we are driving the Fuzz Face’s input with a low impedance source such as another guitar pedal. With the typical pickup model (10k resistor and 2H inductor) placed in series with the signal source the output becomes markedly more symmetric but still spends more time clipped high than low:

It is control over this hard clipped asymmetry (the non-50%-duty cycle) which we implemented in the Vector drive.

Vector Drive Implementation

Before talking about the asymmetry implementation we will look at the Vector Drive’s distortion signal chain. The input signal is fed through a high pass filter to remove any DC offsets (and, if desired, bass frequencies) then into a static non-linearity. The static non-linearity is the equation which dictates the signal clipping shape.

In the Vector Drive the static non-linearity is the equation:

(1) $\begin{equation*}y = \frac{x}{1 + \left| x \right|}\end{equation*}$

which, when plotted, looks like this:

This saturation function is reasonably soft but perfectly capable of producing hard clipped, high gain waveforms as well.

The Fuzz Face’s asymmetry can be produced by adding a vertical offset to the input signal prior to feeding it through the static non-linearity function. There are, however, complications. The result of adding a constant offset of 8 to input sine waves of amplitudes 1 (blue), 10 (green) and 100 (red) is shown below:

The green waveform is as expected, it shows strongly asymmetric soft clipping. However, the effect is lost on the high amplitude sine wave and the low amplitude input has been strongly attenuated. This offsetting method sounds markedly unpleasant as strong signals suddenly jump out and the ability to sustain notes is lost, as audible in the following sound clips:

NB: All the sound clips below have been passed through the Vector Drive’s cabinet modelling filter. No external amplifier has been used. The Vector Drive’s input high pass filter cutoff was set to 100Hz.

Clean recording:

Constant offset clipping:

The solution to the problem above is to measure the input’s amplitude with an envelope follower and add an offset which is proportional to this value. Adding an 80% amplitude offset to the three sine waves above produces this result:

The asymmetry is very similar between the three waveforms and the low amplitude input is only about 6dB below the hard clipped high gain waveform (ie: this method compresses dynamic range in a way we expect a distortion circuit should). The DC offset present in the above waveforms is easily removed with a low frequency (~20Hz) high pass filter.

When this method is applied to the sample riff above it produces a far more musical result. The following samples start with zero offset (just plain distortion saturation) and become “fuzzier” in each clip thereafter:

The Vector Drive allows the offset to be smoothly varied from purely symmetric distortion to super crackly “ripped speaker cone” fuzz. This parameter can be adjusted independently of the other major settings such as the input high pass filter, amplitude symmetry waveshaper and 3ch EQ allow full control of your custom tone creation.